
INTELLIGENT SYSTEM
NEUNGLUETHAI BOORASIT
5537857 EGBE/M
1. To understand the difference between Boolean Logic and Fuzzy Logic, and can give examples for understanding.
2. In order to have a better understanding of the meaning of Membership Function of Fuzzy Logic and Programming MATLAB to create the appearance of the Membership Function.
Crisp value is discrete value or binary value with the true value of 0 or 1.
If set tall men are guy who is taller than 180 cm. Therefore, who is 179 cm tall, that was short because shorter than 180 cm, so the crisp value is 0. But who is 181 cm tall, was tall and a crisp value is 1.
Fuzzy Value is an estimate of the level of data associated with the rule, which is to be a continuous value. The values ranging from 0 to 1, with a value that is the degree of membership function, such as the man is 179 cm tall, the fuzzy value in tall is 0.4 and short is 0.6, while the man is 181 cm tall, fuzzy value in tall is 0.6 but short is 0.4.
Figure1: (a) Crisp value (b) Fuzzy Value
A classical set is a container that wholly includes or wholly excludes any given element. A classical set might be expressed as
A = {x | x > 6}
A fuzzy set is a set without a crisp, clearly defined boundary. It can contain elements with only a partial degree of membership. A fuzzy set A in X is defined as a set of ordered pairs
A = {x, µA(x) | x ∈ X}
µA(x) is called the membership function of x in A. The membershipfunction maps each element of X to a membership
value between 0 and 1.
Classical sets and Fuzzy sets
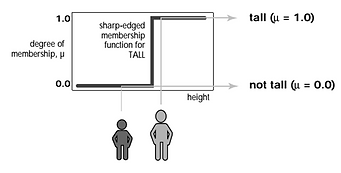

Figure2: (a) Classical Set (b) Fuzzy Set
Boolean logic and Fuzzy logic
Boolean Logic is based on the algebra of truth values, all values are true or false (0 or 1) it will not be possible for one thing to have a truth-value may or may not be. It is usually found on a computer that has a binary number in the calculation.
Fuzzy Logic is logic similar to the human mind. Everything is looking up on the basis of probability. The truth from 0 to 1 (0% to 100%), as the weather today, it may be raining 30%, indicating that there is a chance that rain will not fall by 70% as well.
How beautiful i am in terms of fuzzy logic and Boolean logic
For the question that how beautiful i am in term of Boolean logic, it has only 2 answers, beautiful or not beautiful. So i can say that I'm beautiful.
But for fuzzy logic is based on the concept and perspective of the individual. Each of them will have to break at different levels. May be classified as unattractive, so-so, beautiful little, beautiful moderate, beautiful, very beautiful and beautiful as possible. So i think that I was in the middle of it.
The membership function of my beautiful logic in both cases
In Boolean logic, the membership function of my beautiful are 0 and 1 . But for fuzzy logic, the membership function of my beautiful are 0 for unattractive, 0.2 for so-so, 0.4 for beautiful little, 0.5 for beautiful moderate, 0.6 for beautiful, 0.8 for very beautiful and 1.0 for beautiful as possible.


Figure3: (a) Membership function of Boolean Logic (b)Membership function of Fuzzy Logic
Two forms of fuzzy representation
Fuzzy set can be represented into two forms.
Let X is a universe of discourse
x is an element in X
A is a fuzzy set
µA is a membership of x in the fuzzy set A
First Form :
Example : Fuzzy set A = “sensible number of children”
X = {0, 1, 2, 3, 4, 5, 6} (discrete universe)
A = {(0, 0.1), (1, 0.3), (2, 0.7), (3, 1.0), (4, 0.6), (5, 0.2), (6, 0.1)}
Second Form :
Example : Fuzzy set A = “sensible number of children”
X = {0, 1, 2, 3, 4, 5, 6} (discrete universe)
A = 0.1/0 + 0.3/1 + 0.7/2 + 1.0/3 + 0.6/4 + 0.2/5 + 0.1/6


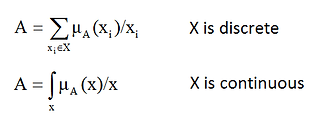
Basic terms and Operations of Fuzzy logic
Support is a part of the universe that has value of the member function greater than 0.
Core is a part of the universe that has value of the member function equal to 1.
Boundary is a part of the universe that has value of the member function between 0 and 1.
Normal fuzzy set is a set that has at least one element in the universe whose membership value is equal to 1.
Convex fuzzy set is a set that in one curve has membership value increasing and decreasing just one time.
Figure4 : (a) convex and normal fuzzy set (b) nonconvex but normal fuzzy set
Empty fuzzy set is a set that all of elements have degree of membership equal to 0.
Identity
A ∪ Ø = A A ∪ X = X
A ∩ X = A A ∩ Ø = Ø
Example, for A = {0, 1, 2}
the universal relation(denoted UA), and the identity relation(denoted IA), are found to be
UA = {(0, 0), (0, 1), (0, 2), (1, 0), (1, 1), (1, 2), (2, 0), (2, 1), (2, 2)}.
IA = {(0, 0), (1, 1), (2, 2)}
Complement in fuzzy set is NOT
Complement μR(x, y) = 1 − μR(x, y)
Fuzzy number If A is a convex single-point normal fuzzy set defined on the real line, then A is often termed a fuzzy number.

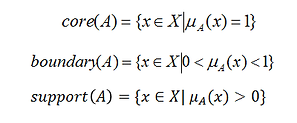

MATLAB programming of membership function
Triangular membership function is defined by the parameters [a b c],
where a is the membership function's left intercept with grade equal to 0
b is the center peak where the grade equals 1
c is the right intercept at grade equal to 0.
Trapezoidal membership function, trapmf, has a flat top and really is just a truncated triangle curve. It is defined by the parameters [a b c d], parameters a and d locate the "feet" of the trapezoid and the parameters b and c locate the "shoulders".
Gaussian membership function is popular methods for specifying fuzzy sets, the curves has the advantage of
being smooth and nonzero at all points. It depends on two parameters [sig c].
Sigmoidal membership function, which is either open left or right. It depends on two parameters [a c].

Figure5 : MATLAB Programming of memership function
Discussion
Fuzzy logic is superset of Boolean logic, so if you understand about crisp value and operations of its, you could be understand in fuzzy set too. Fuzzy sets have own characteristics like empty fuzzy set, normal fuzzy set, convex fuzzy set, identity and complement. From this assignment makes me to understand about fuzzy number and i can write MATLAB code to create a membership function of fuzzy set.
Neungluethai Boorasit 5537857 EGBE/M