
INTELLIGENT SYSTEM
NEUNGLUETHAI BOORASIT
5537857 EGBE/M
Objectives
1) To understand fuzzy numbers Using alpha-cut representation and the extension principle.
2) To know the different between crisp relations and fuzzy relations.
3) Can give an example to representation fuzzy relations.
4) To know what is composition of fuzzy relation and can give an example of its.
Fuzzy Numbers
There are two fuzzy numbers,
A = 3 = 0.3/1 + 0.7/2 + 1/3 + 0.7/4 + 0.3/5 B = 7 = 0.2/5 + 0.6/6 + 1/7 + 0.6/8 + 0.2/9
can represent in table1 for easy to understand

Table1. Fuzzy numbers about3 and about7
Addition
Using alpha-cuts representation Using the extension principle



Figure1.1 addtion using alpha-cuts
Figure1.2 addtion using extension principle
From figure1.1, show the result of addtion fuzzy numbers about3 and about7 is about10 because number10 has degree of membership equal to 1.
From figure1.2, the result show that summation of number3 from fuzzy set A and number7 from fuzzy set B is equal to 10 and degree of number 10 is 1.0 so about10 is the result from this addition.
Thus C = A+B = 0.2/6 + 0.3/7 + 0.6/8 + 0.7/9 + 1.0/10 + 0.7/11 + 0.6/12 + 0.3/13 + 0.2/14
Subtraction
From figure2.1, show the result of subtraction fuzzy numbers about3 and about7 is about -4 because number -4 has degree of membership equal to 1.
From figure2.2, the result show that subtraction of number3 from fuzzy set A and number7 from fuzzy set B is equal to -4 and degree of number -4 is 1.0 so about -4 is the result from this subtraction.
Thus C = A-B = 0/-9 + 0.2/-8 + 0.3/-7 + 0.6/-6 + 0.7/-5 + 1/-4 + 0.7/-3 + 0.6/-2 + 0.3/-1 + 0.2/0 + 0/1
Using alpha-cuts representation Using the extension principle



Figure2.1 subtraction using alpha-cuts
Figure2.2 subtraction using extension principle
Multiplication
Using alpha-cuts representation Using the extension principle

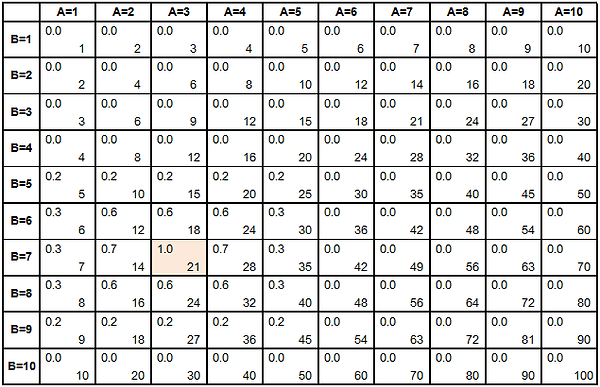
Figure3.1 Multiplication using alpha-cuts
Figure3.2 Multiplication using extension principle
From figure3.1, show the result of multiplication fuzzy numbers about3 and about7 is about 21 because number 21 has degree of membership equal to 1.
From figure3.2, the result show that multiplication of number3 from fuzzy set A and number7 from fuzzy set B is equal to 21 and degree of number 21 is 1.0 so about 21 is the result from this multiplication.
Division
Using alpha-cuts representation Using the extension principle



Figure4.1 Division using alpha-cuts
Figure4.2 Division using extension principle
From figure4.1, show the result of division fuzzy numbers about3 and about7 is about 0.4 because nearest number 0.4 has degree of membership equal to 1.
From figure4.2, the result show that division of number3 from fuzzy set A and number7 from fuzzy set B is nearest to 0.4 and degree of nearest 0.4 is 1.0 so about 0.4 is the result from this dvision.
Relation means to describe the relationship between the data from two or more sets. The crisp relation has degree of association is 0 or 1. But for fuzzy relation has degree of association between 0 and 1.
Fuzzy relation is a link between 2 or more fuzzy sets will be based on the degree of membership which can be applied to fuzzy clustering, fuzzy control and fuzzy reasoning as well as to evaluate and compare an important of the problem with such a fuzzy diagnosis and fuzzy modeling.
Fuzzy relation is fuzzy if / then rules by specifying that one thing is the element of another. The order of relationships will be important as well.
Example
Crisp set X with three linguistic terms is given as
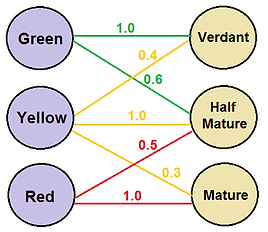
X = {green, yellow, red}
Similarly the grade of maturity for the other set Y will be
Y = {verdant, half-mature, mature}
Crisp formulation of a relation X to Y between two crisp sets is presented in tabular form
The figure5.2 represents the fuzzy relation.
Fuzzy Relations


Figure5.1 Crisp relations
Figure5.2 Fuzzy relations
Fuzzy Relation Representations
From an example of fuzzy relation in figure5.2 can described in 5 ways
1) Tabular form 2) Matrix form


3) Direct Graph form


4) Linguistically, “x divides y”
5) By listing the set of all ordered pairs
Projection of Fuzzy Relation
From fuzzy relation R(x,y)
The projection of R(x,y) on X denoted by
and The projection of R(x,y) on Y denoted by
Example
From previous fuzzy relation
The projection of R(x,y) on X is calculated as
so the X projection is
The projection of R(x,y) on Y is calculated as
so the Y projection is


Cylindrical extension of Fuzzy Relation
Cylindrical extension from X-projection means filling all the columns of the related matrix by theX -projection.
Similarly cylindrical extension from Y projection means filling all the rows of the relational matrix by the Y -projection.
Example
From the fuzzy relation
The projection of R(x,y) on X is calculated as
so the X projection is
So The cylindrical extension of R1 is
The projection of R(x,y) on Y is calculated as
so the Y projection is
So The cylindrical extension of R2 is





Fuzzy Max-Min Composition
Let us consider two fuzzy relations R1 and R2 defined on a Cartesian space X x Y and Y x Z respectively. The max-min composition of R1 and R2 is a fuzzy set defined on a cartesian spaces X x Z as
Example
Let R1(x,y) and R2(y,z) be defined as the following relational matrices
the max-min composition can be
calculated each entries
The relational matrix for max-min composition in fuzzy relation is thus





Fuzzy Max-Product Composition
Max-Product composition is similar to Max-Min composition but its different at try to multiply between two value of degree of membership instead of to do minimum
Example
Let R1(x,y) and R2(y,z) be defined as the following relational matrices
the max-product composition can be
calculated each entries
The relational matrix for max-product composition in fuzzy relation is thus





Fuzzy Max-Average Composition
Max-Average composition has method like this. First, do the summation of two degree or membership. Then, find the maximum value. Finally, give the average of maximum value divided by 2.
Example
Let R1(x,y) and R2(y,z) be defined as the following relational matrices
the max-average composition can be
calculated each entries
The relational matrix for max-average composition in fuzzy relation is thus




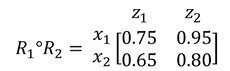
Discussion
From this assignment, i know about fuzzy relation, fuzzy composition and fuzzy number operation. But i'm not sure that my understanding is correct or not because i'm too confuse about it. For fuzzy number operation, i try to coding with MATLAB but it has some error in subtraction and division that i can't solve it so i change to describe it like table by hand addition. Finally, this assignmnet make me feel good with fuzzy because i read a lot and familiar with it and the last, i want to say i'm so sorry about my grammar.
Neungluethai Boorasit
5537857 EGBE/M
