
INTELLIGENT SYSTEM
NEUNGLUETHAI BOORASIT
5537857 EGBE/M
Objectives
1) Can write program about the membership function of fuzzy set by using equations that have got.
2) To understand fuzzy operations and fuzzy modifiers by using MATLAB function.
3) Can explain Extension principle, Alpha cut and Resolution principle.
Create membership function from two fuzzy sets
fuzzy set A :
fuzzy set B :



MATLAB Code
Universe=0:0.5:20;
MFA=1./(1+((Universe./5).^3));
MFB=1./(1+(0.3*(Universe-8).^2));
figure1. Membership function of set A and B
AND & OR operation
AND operation :
OR operation :

MATLAB Code
AandB=min(MFA,MFB);
AorB =max(MFA,MFB);
figure2. Membership function of A AND B (left) Membership function of A OR B (right)


Properties of fuzzy sets
Properties related to Union
Identity : A∪∅=A
A∪X=X
Idempotence : A∪A=A
Commutativity : A∪B=B∪A
Associativity : A∪(B∪C)=(A∪B)∪C
Additional Properties
Distributivity : A∩(B∪C)=(A∩B)∪(A∪C)
A∪(B∩C)=(A∪B)∩(A∪C)
Law of excluded middle : A∪A′=X
Law of contradiction : A∩A′=∅
Properties related to Intersection
Absorbtion by empty set : A∪∅=∅
Identity : A∩X=A
Idempotence : A∩A=A
Commutativity : A∩B=B∩A
Associativity : A∩(B∩C)=(A∩B)∩C
Modifiers of fuzzy set
MATLAB Code
VeryA = MFA.^2;
MoreOrLessA = MFA.^(1/2);
IndeedA = 1:length(Universe);
for n = 1:length(Universe)
if MFA(n)>=0 && MFA(n)<=0.5
IndeedA(n) = 2*(MFA(n)^2);
else MFA(n)>=0.5 && MFA(n)<=1
IndeedA(n) = 1-(2*(1-(MFA(n))^2));
end
end
NotA = 1-MFA;


figure3. Membership function of fuzzy modifiers
Extension Principle

- Provides a general procedure for extending crisp domains of mathematical expressions to fuzzy domains.
- Generalizes a common point-to-point mapping of a function to a mapping between fuzzy sets.
the general function f: X → Y
A function mapping fuzzy subset of X into fuzzy subset of Y.
If x is the level of μ, then y = f (x) is assigned to the level of membership μ.
[If more than one x is mapped into y then the maximum of such memberships is used as the definition of the degree of membership of y]
figure4. Mapping of conventional sets (left) and Mapping of fuzzy sets (right)
Suppose that f is a function from X to Y and A is a fuzzy set on X defined as:
The extension principle states that the image of fuzzy set A under the mapping f(.) can be expressed as a fuzzy set B.
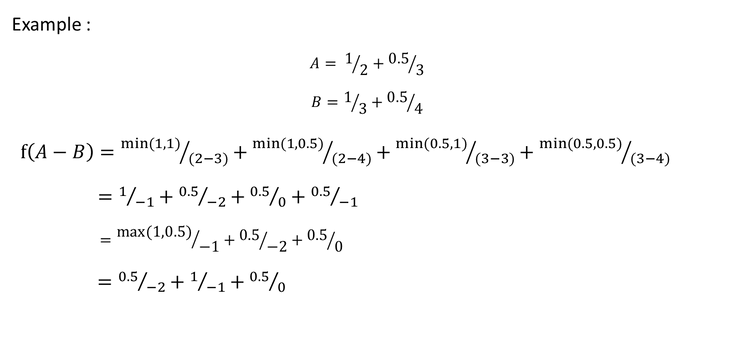
Alpha cuts
Alpha cut is a crisp set that contained of elements of A which has a degree of membership more than alpha
Example :

This principle offers a way of representing membership to fuzzy sets by means of alpha cuts.
The maximum is taken over all alpha cut, and the equation indicates that the membership function of A is the union of all alpha cut, after each one of them has been multiplied by alpha.
Resolution Principle

figure5. Membership function of A by alpha cut
Discussion
From an assignment4, I can understand some properties and some operations of fuzzy set and i can write MATLAB code to see how the membership function will be. AND and OR operations are common use in fuzzy algorithm and now i know that AND operation is minimize of membership function same as intersection and OR operation is try to maximize of membership function same as union. But i have some part that i'm not sure about it like resolution principle and extension principle so i try to study it harder to understand it.